二.C语言中的数据类型

发表于 | 分类于 | | 阅读次数

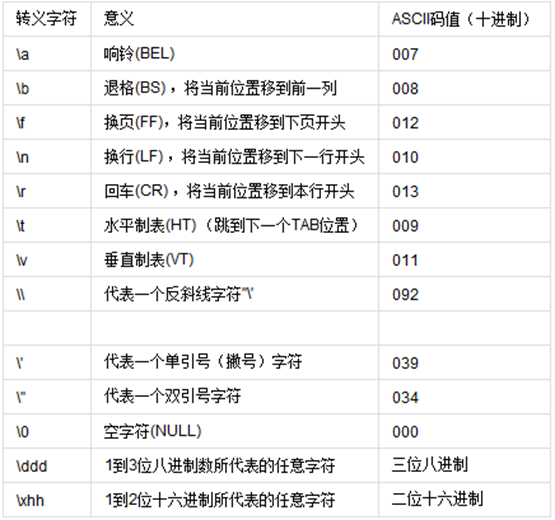
1. 转义字符

转义字符

1.1 演示代码

1
2
3
4
5
6
7
8
9
10
11
12
13
#include<stdio.h>
#include<stdlib.h>
#include<Windows.h>
void main() {
	while (-1) {
		putchar('\x42');//16  4*16+2=66
		putchar('\a');//发声
		Sleep(1000);
		system("\"D:\\Program Files (x86)\\Tencent\\QQ\\Bin\\QQScLauncher.exe\"");
		putchar('\0');
	}
}

2. 什么是变量与常量

  • 常量就是计算机内存里面不变得数据

  • 变量就是计算机内存里面需要并且经常改变的数据

变量是指其值可以变化的量.计算机中,指令代码/数据都存储于内存中.变量也需要存储在内存中.在计算机中,每个变量都被分配了一块内存空间,在这些空间里存储的就是变量的值.变量之所以可以变化,就是这个存储空间可以存储不同的数值.存储空间里的值变化,则变量对应的值也变化.同一个时间,内存空间里只能保存一份值,新值冲掉了原来的旧值.每个内存单元都有编号,这些是内存的地址.

1
2
3
4
5
6
7
8
9
10
11
12
void main() {
	int a = 10;
    //这段代码表示了从寄存器修改数据
	_asm {
		mov eax,8
		mov a,eax
	}
	printf("%p\n", &a); //%p 是以16进制的形式输出内存地址
	printf("%d", a);
	getchar();
}

2.1 定义变量

  • 标识符
    • 定义 :
      程序中用于标识常量、变量、函数的字符序列
    • 组成 :
      只能由字母/数字/下划线组成,第一个字母必须是字母或下划线,大小写有区别
      不能使用C语言的关键字.
    • 规则 :
      见名知意
      不宜混淆

2.1.1 变量为何一定要初始化

变量如果不初始化,可以编译成功,但是执行的时候,很可能报错 .

操作系统是如何管理内存的!

每当一个应用程序打开时,操作系统为其分配内存,内存有内存地址与内存单元,当应用程序初始化运行时,就会往内存单元里面写数据,当操作系统回收的时候,并不清空内存单元,所以存在大量的垃圾数据.

如果变量不初始化,就会默认读取垃圾数据,有些垃圾数据会导致程序崩溃.
VC++2010的编译器可以感知变量没有初始化,调试的时候就会出错.
所以,变量使用之前,必须初始化.

2.1.2 变量交换

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
void main1() {
	int a = 10;
	int b = 5;
	int temp;
	printf("a=%d,b=%d\n", a, b);
	printf("交换后:\n");
	temp = a;	//temp = 10;a = 10; b = 5;
	a = b;	//temp = 10;a = 5; b = 5;
	b = temp; // temp = 10;a = 5; b = 10;
	printf("a=%d,b=%d\n", a, b);
	getchar();
}
void main() {
	int a = 10;
	int b = 5;
	printf("a=%d,b=%d\n", a, b);
	printf("交换后:\n");
	a = a ^ b;	//a=15,b=5
	b = a ^ b;	//a=10,a=15
	a = a ^ b;	//a=5,b=10
	printf("a=%d,b=%d\n", a, b);
	getchar();
}

2.2 定义常量

  • 定义常量有什么好处呢?
    • 通过有意义的单词符号,可以指明该常量的意思,使得程序员在阅读代码时,减少迷惑.
    • 需要修改常量的时候,可以只需要修改一次,实现批量修改,效率高而且准确.
1
2
3
4
5
6
7
8
9
10
11
12
13
#include<stdio.h>
#include<stdlib.h>
#include<Windows.h>
#define 诸葛亮	100
void main() {
	//真正的常量,不能直接修改!因为C语言只能操作内存,不能操作寄存器
	const int a = 1000;
	printf("%d\n",诸葛亮);
	printf("%d\n", a);
	getchar();
}

3. 进制问题

3.1 进制的计算

进制转换

3.2 二进制转换八进制

  • 二进制转换成八进制 : 从右向左,每3位一组(不足3位左补0),转换成八进制
    (1101001)2=(001,101,001)2=(151)8
  • 八进制转换成二进制 : 用3位二进制数代替每一位八进制数.
    (246)8=(010,100,110)2=(10100110)2

3.3 二进制转换十六进制

  • 二进制转换成十六进制 : 从右向左,每4位一组(不足4位左补0),转换成十六进制
    (11010101111101)2=(0011,0101,0111,1101)2=(357D)16
  • 十六进制转换成二进制 : 用4位二进制数代替每一位十六进制数
    (4B9E)16=(0100,1011,1001,1110)2=(100101110011110)2

    0000 ~ 0
    0001 ~ 1
    0010 ~ 2
    0011 ~ 3
    0100 ~ 4
    0101 ~ 5
    0110 ~ 6
    0111 ~ 7
    1000 ~ 8
    1001 ~ 9
    1010 ~ A
    1011 ~ B
    1100 ~ C
    1101 ~ D
    1110 ~ E
    1111 ~ F

3.4 十进制转换二进制

  • 十进制整数转换为二进制 : 方法是除以2取余,逆序排列,以(89)10为例,如下.
    89 ÷ 2 余1
    44 ÷ 2 余0
    22 ÷ 2 余0
    11 ÷ 2 余1
    5 ÷ 2 余1
    2 ÷ 2 余0
    1 余1
    (89)10 = (1011001)2
    (5)10 = (101)2
    (2)10 = (10)2

  • 二进制转换为十进制
    十进制是逢十进一,由数字符号0,1,2,3,4,5,6,7,8,9组成,可以这样分析十进制数 :
    (1234)10 = 1 10^3 + 2 10^2 + 3 10^1 + 4 10^0 = 1000 + 200 +30 + 4 =(1234)10

  • 采用同样的方式转换二进制到十进制
    (1101)2 = 1 2^3 + 1 2^2 + 0 2^1 + 1 2^0 = 8 + 4 + 0 + 1 = (13)10
    (10.01)2 = 1 2^1 + 0 2^0 + 0 2^-1 + 1 2^-2 = 2 + 0 + 0 + 0.25 = (2.25)10

  • 十进制小数的转换为二进制 : 方法是乘以2取整,顺序排列,以(0.625)10为例,如下 :
    0.625 2 = 1.25 取整1
    0.25     2 = 0.5 取整0
    0.5 * 2 = 1 取整1
    (0.625)10 = (0.101)2
    (0.25)10 = (0.01)2
    (0.5)10 = (0.1)2

4. 计算机存储数据

程序员编写的程序以及所使用的数据在计算机的内存中是以二进制位序列的方式存放的.

典型的计算机内存段二进制位序如下 :
…0001000101010101000101010111011001010010100100010010010010….

上面的二进制位序里,每一位上的数字,要么是0,要么是1.在计算机中,位(bit)是含有0或者1值的一个单元.在物理上,它的值是一个负或是一个正电荷.也就是计算机中可以通过电压的高低来表示一位所含有的值.如果是0,则用低电压表示,如果是1,则用高电压表示.

在上面的二进制位序这个层次上,位的集合没有结构,很难来解释这些系列的意义.为了能够从整体上考虑这些位,于是给这些位序列强加上结构的概念,这样的结构被称作为字节(byte)和字(word).通常,一个字节由8位构成,而一个字由32位构成.或者说是4个字节构成。

5. sizeof运算符

sizeof是个单目运算符,用来计算操作数在内存中占据的字节数,其操作数既可以是括在圆括号中的类型标识符,其返回值是size_t类型,即无符号整数.

1
2
3
4
5
6
sizeof(short);				/*返回2*/
sizeof(long);				/*返回4*/
sizeof(int);	       /*不确定，取决于不同的系统*/
也可以是一个表达式，如：
short x；
sizeof(x);					/*返回2*/

6. 原码和反码和补码

原码 反码 补码
+7 00000111 00000111 00000111
-7 10000111 11111000 11111001
+0 00000000 00000000 00000000
-0 10000000 11111111 00000000
数的范围 01111111~11111111(-127~+127) 01111111~10000000(-127~+127) 01111111~10000000(-128~+127)

负数补码转换成十进制数 : 最高位不动,其余位取反加1.

补码 : 11111001
取反 : 10000110
加1 : 10000111=-7

数值的表示方法——原码/反码和补码

  • 原码 : 最高位为符号位,其余各位为数值本身的绝对值
  • 反码 :
    正数 : 反码与原码相同
    负数 : 符号位为1,其余位对原码取反
  • 补码 :
    正数 : 原码 / 反码 / 补码相同
    负数 : 最高位为1,其余位为原码取反,再对整个数加1

在计算机系统中,数值一律用补码来表示(存储). 主要原因 : 使用补码,可以将符号位和其它位统一处理;同时,减法也可按加法来处理.另外,两个用补码表示的数相加时,如果最高位(符号位)有进位,则进位被舍弃.

采用原码表示法简单易懂,但它的最大缺点是加法运算复杂.这是因为,当两数相加时,如果是同号则数值相加;如果是异号,则要进行减法.而在进行减法时还要比较绝对值的大小,然后大数减去小数,最后还要给结果选择符号.为了解决这些矛盾,人们找到了补码表示法.机器数的补码可由原码得到.如果机器数是正数m则该机器数的补码与原码一样;如果机器数是负数,则该机器数的补码是对它的原码(除符号位外)各位取反,并在未位加1而得到的.

7. 总结与练习

  • 计算 :
    • 十进制192 到二进制 : 11000000
    • 十进制62 到二进制 : 111110
    • 二进制1111001001010 到十进制 : 7754
    • 二进制1111101111010 到十进制 : 8058
    • 0.5转化为二进制 : 0.1
    • 1.25转换为二进制 : 1.01
  • 推理运算结果 :
1
2
3
4
5
6
7
8
9
10
11
12
13
int num = -2;
unsigned int data = 4294967294u;
int num1 = 4294967294u;
unsigned int data1 = -2;
printf("%d", num);  //-2
printf("\n%u", num); //4294967294
printf("\n%d", num1); //-2
printf("\n%u", num1); //4294967294
printf("\n%u", data); //4294967294
printf("\n%d", data); //-2
printf("\n%u", data1); //4294967294
printf("\n%d", data1); //-2